Hi Jean-Francois. You're welcome - well, again this isn't an answser, but my comment wouldn't fit in a comment :-| Curve fitting is a big subject area which you'd need to research a bit more on your own. Here's some ways to head out: almost any 2 dimensional curve can be generated using polynomial equations. Take for example a basic parabola, y = x^2. Each x value generates a y. This process can be reversed. Any set of points, if they are not too chaotic or random, can be used to 'connect the dots' making a curve. If you fit your image data points (you know now the y, but need to figure out the x ), you can figure out :)) what figure it is. So how to get the image points? If, as Sammy suggests, you get the crescent to stand out enough, you can use the black/white transistion pixels, either to make a filled form (meaning you don't care about whats 'inside' the crescent), or, create a shadow line drawing. (There's also a set of opencv routines that do this, but I don't recall their name - maybe someone can chime in here.) It's like a hit or miss, like the mine sweeper game ... your points will be on one or the other side of the "edge" of the crescent, then you use those points to 'regress' and refine the actual location of the edges. Once you have an x,y matrix of points, you can figure out the polynomial equation. If the curve edge of the crescents are smooth and circle like, then you only need the polynomial for a partial circle, used twice - one for the inner (partial) circle, and one for the outer. The only difference is the radii of the two. - H
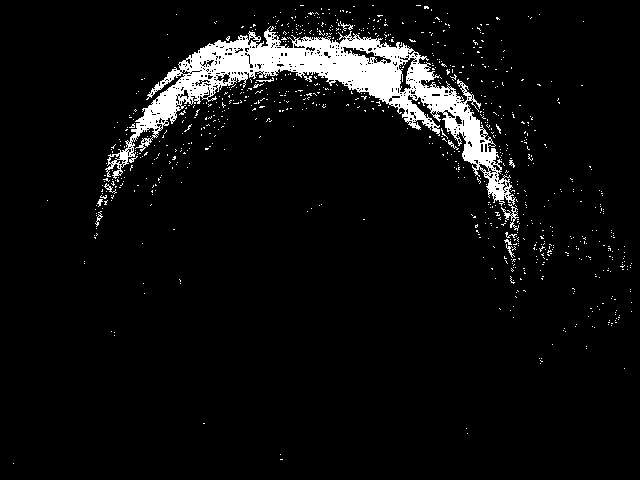


a general observation, not an answer per se. First (and obviously) mask out the noise and "other" shapes as best you can. Assuming the input data is strictly a "crescent" - that is two circles of differing diameter, joined at two common points - you could find the common points of intersection, then treat the two 'edges' as simple 2-d polynomial curves. Do multiple linear regression on each curve until they " fit " ... if your curves are generic enough, a simple data set would be your baseline to compare against. HTH - HP
Hi Howard. Thanks for the observation. Could you write an answer and go deeper into the explanation about the detection of the 2 edges and how to do a 2D polynomial curve?