Recently, I have been studying the pinhole camera model for several days but I was confused with the model provided by OpenCV and "Multiple View geometry in computer vision" which is a famous textbook.
I know that the following photo is a simplified model which switches the position of the image plane and the camera frame. Basically,for better illustration and understanding and Taking consideration of the principal point (u0,v0), the relation between two frames is
x=f(X/Z)+u0 and
y=f(Y/Z)+vo.
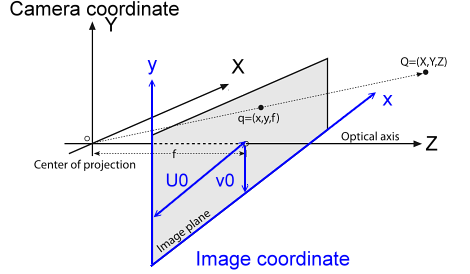
However,I was really confused because normally the image coordinate is in the form of the 4th quadrant coordinate as the following one!
Could I directly substitute the (x,y) in the following definition to the above "equivalent" pinhole model which is not really persuasive?
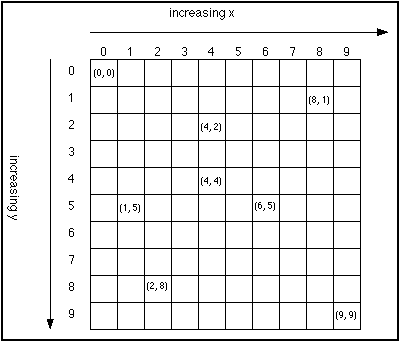
Besides, If an object is in the region (+X,+Y) quadrant in the camera coordinate (of course, Z>f), in the equivalent model, it should appear on the right-half plane of the image coordinate. However, such object in the image taken by a normal camera, it is supposed to be located on the left-half. Therefore, for me this model is not reasonable.
Finally, I tried to derive based on the original model as the following one.
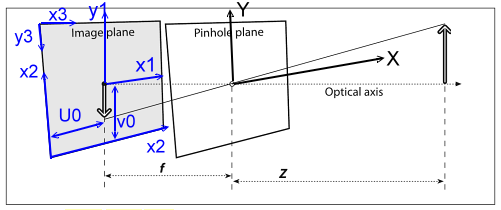
The result is
x1=-f(X/Z) and
y1=-f(Y/Z). Then, I tried to find the relation between (x2,y2)-coordinate and the camera coordinate. The result is
x2=-f(X/Z)+u0 and
y2=-f(Y/Z)+vo.
Between (x3,y3)-coordinate and the camera coordinate, the result is
x3=-f(X/Z)+u0 and
y3=f(Y/Z)+vo.
no matter which coordinate system i tried, none of them is in the form of
x=f(X/Z)+u0 and
y=f(Y/Z)+vo, which are provided by some CV textbooks.
Besides, the projection results on (x2,y2)-coordinate or (x3,y3)-coordinate are also not reasonable because of the same reason- an object in the (+X,+Y,+Z) region in the camera coordinate should "appear" on the left-half plane of the image taken by a camera.
Could anyone indicate what I was misunderstood with and I will try to derive several times more and post the answer when someone else help me figure this issue out.
Thank you in advance!!
Alex

