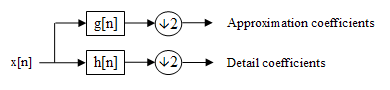
I have two question 1 : what is the high pass filter of 1D haar wavelet transform??
2 : Is this a correct way to apply wavelet transform
According to the wikipedia, 1D wavelet transform can be done by simple convolution. Ex : x[] = {1 2 3 4}, hfilter[] = {1, -1}, hfilter_inv[] = {-1, 1}
y[0] = x[0] * 1; y[1] = x[0] * -1 + x[1] * 1; y[2] = x[2] * -1 + x[2] * 1; y[3] = x[3] * -1 + x[3] * 1;
after down sampling, y[0] = x[0] * 1; y[1] = x[1] * -1 + x[2] * 1;