I need to retrieve the attitude angles of a camera (using cv2 on Python).
- Yaw being the general orientation of the camera when on an horizontal plane: toward north=0, toward east = 90°, south=180°, west=270°, etc.
- Pitch being the "nose" orientation of the camera: 0° = horitzontal, -90° = looking down vertically, +90° = looking up vertically, 45° = looking up at an angle of 45° from the horizon, etc.
- Roll being if the camera is tilted left or right when in your hands: +45° = tilted 45° in a clockwise rotation when you grab the camera, thus +90° (and -90°) would be the angle needed for a portrait picture for example, etc.
I have yet rvec and tvec from a solvepnp().
Then I have computed:
rmat = cv2.Rodrigues(rvec)[0]
If I'm right, camera position in the world coordinates system is given by:
position_camera = -np.matrix(rmat).T * np.matrix(tvec)
But how to retrieve corresponding attitude angles (yaw, pitch and roll as describe above) from the point of view of the observer (thus the camera)?
I have tried implementing this : http://planning.cs.uiuc.edu/node102.html#eqn:yprmat in a function :
def rotation_matrix_to_attitude_angles(R) :
import math
import numpy as np
cos_beta = math.sqrt(R[2,1] * R[2,1] + R[2,2] * R[2,2])
validity = cos_beta < 1e-6
if not validity:
alpha = math.atan2(R[1,0], R[0,0]) # yaw [z]
beta = math.atan2(-R[2,0], cos_beta) # pitch [y]
gamma = math.atan2(R[2,1], R[2,2]) # roll [x]
else:
alpha = math.atan2(R[1,0], R[0,0]) # yaw [z]
beta = math.atan2(-R[2,0], cos_beta) # pitch [y]
gamma = 0 # roll [x]
return np.array([alpha, beta, gamma])
but it gives me some results which are far away from reality on a true dataset.
Am I doing something wrong?
And if yes, what?
All informations I've found are incomplete (never saying in which reference frame we are or whatever in a rigorous way).
Thanks.


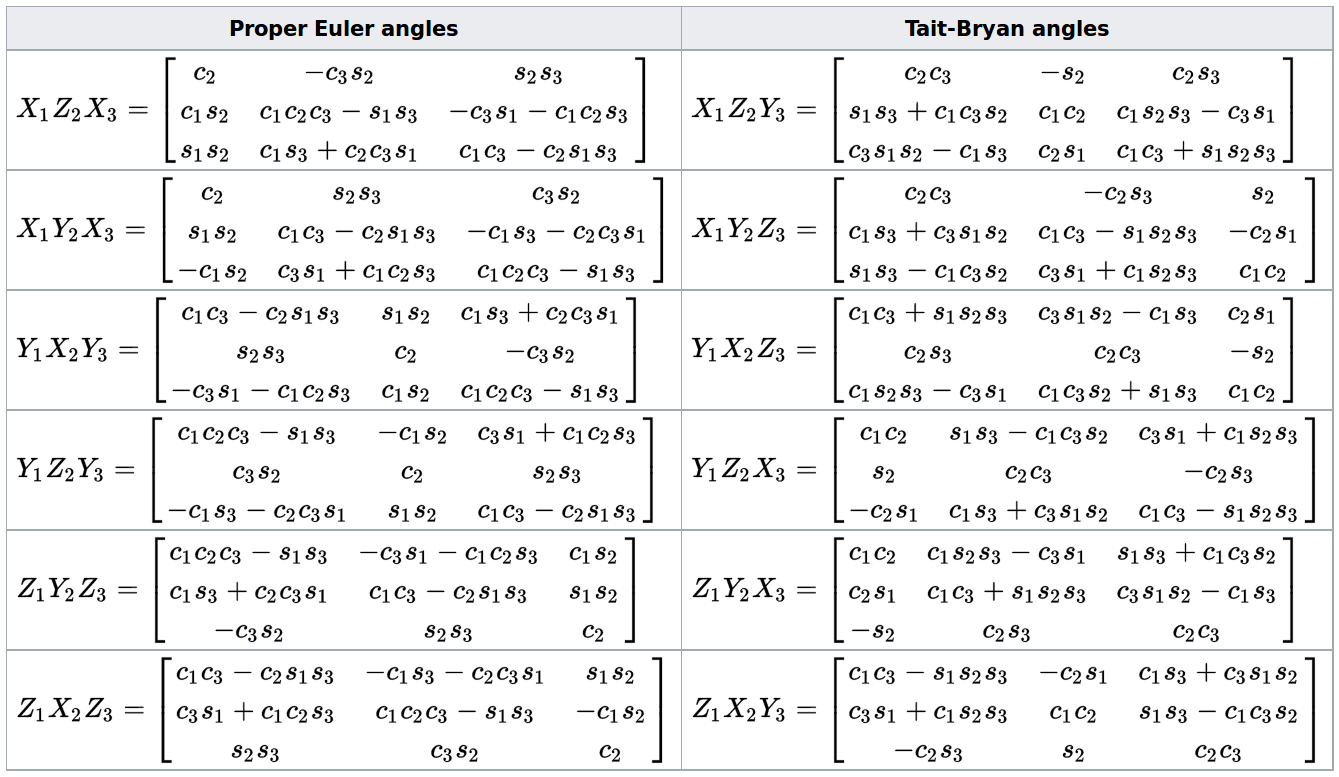 From: https://en.wikipedia.org/wiki/Euler_angles
From: https://en.wikipedia.org/wiki/Euler_angles