How to do a 3d->2d back projection
I am trying to calibrate a stereo camera setup. I use images from multiple chessboards from two cameras. I get corner points for all images and use these to run separate camera calibrations. This I can use to do pose estimation as shown in the documentation example. I however cannot figure out how to triangulate points and do a back projection of the 3d points to the separate 2d images. This is the example from the documentation for a single camera:
_,rvecs0, tvecs0, inliers = **cv2.solvePnPRansac****(objp, imgpoints3, mtx0, dist0)
imgpts, jac = cv2.projectPoints(axis, rvecs0, tvecs0, mtx0, dist0)*
This works perfectly, but uses the rotation and translation vectors for a single pose. My question is how to generalise this, without using the pose of a calibration plane?
I have used the stereo calibration function and stereo rectify functions to obtain the required parameters for triangulation and for projectpoints, but this is where I get stuck:
retval, cameraMatrix0, distCoeffs0, cameraMatrix1, distCoeffs1, R, T, E, F= cv2.stereoCalibrate( np.array(objpoints), np.array(imgpoints0), np.array(imgpoints1), mtx0, dist0, mtx1, dist1, img_shape, flags= cv2.CALIB_FIX_INTRINSIC )
R0, R1, P0, P1, dum, dum, dum = cv2.stereoRectify(cameraMatrix0, distCoeffs0, cameraMatrix1, distCoeffs1,img_shape, R,T)
What should now be the sequence of calls to calculate 3d points, and get a back projection in the separate images for the 3d points?
My closest solution is:
in0 = cv2.undistortPoints( in00, cameraMatrix0, distCoeffs0, P=cameraMatrix0 ) in1 = cv2.undistortPoints( in11, cameraMatrix1, distCoeffs1, P=cameraMatrix1)
points3d = cv2.triangulatePoints(P0, P1, in0, in1) (with projection matrix from stereo rectify function)
points3d=cv2.convertPointsFromHomogeneous(points3d) 3.5 inpoints=np.transpose(np.squeeze(np.transpose(points3d),1)) #reshape the 3d points
imgpts0, jac = cv2.projectPoints(inpoints,(0, 0, 0), (0, 0, 0), cameraMatrix0, distCoeffs0) imgpts1, jac = cv2.projectPoints(inpoints,R, T, cameraMatrix1, distCoeffs1)
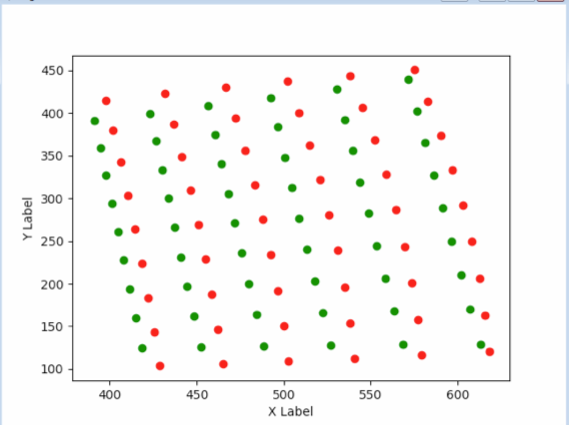
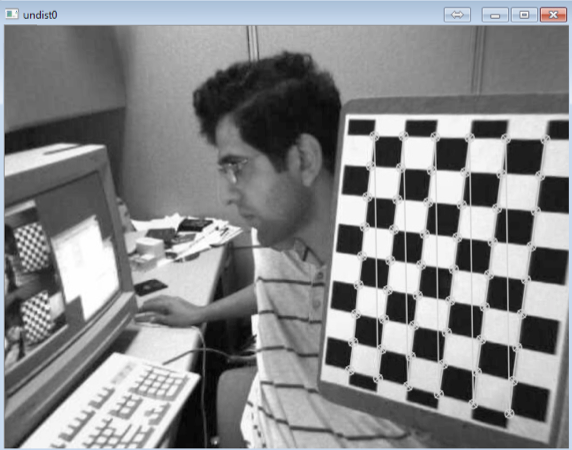
This works somehow but the scaling is off and the error is far too large. Also, if I do a re-triangulation of the back-projected points I do not get the same 3d coordinates back! Somehow I am not dealing appropriately with the distortion it seems, but the un-distortion works perfectly (checked from undistorted images and undistorted points in overlay). The images show the error (difference between red and green points, and an example of successful un-distortion.
Any ideas where I go wrong are welcome!