This forum is disabled, please visit https://forum.opencv.org
 | 1 | initial version |
What you are looking for is called Homogeneous transformation matrix.
To get the 3D coordinate of the camera in the poster frame, assuming a known camera pose, you just have to compute what is called the inverse of the homogenous matrix (see this course, page 72).
 | 2 | No.2 Revision |
What you are looking for is called Homogeneous transformation matrix.
To get the 3D coordinate of the camera in the poster frame, assuming a known camera pose, you just have to compute what is called the inverse of the homogenous matrix (see this course, page 72)., Ridig Body Motion – Homogeneous Transformations by Claudio Melchiorri).
I strongly recommend to read a course about homogeneous transformation (the one linked should be good).
I recall the equations in case the link is no more accessible.
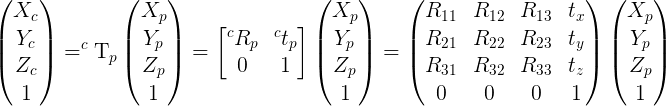
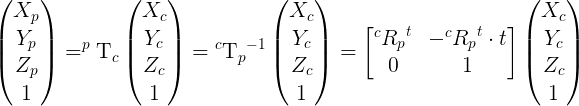
 | 3 | No.3 Revision |
What you are looking for is called Homogeneous transformation matrix.
To get the 3D coordinate of the camera in the poster frame, assuming a known camera pose, you just have to compute what is called the inverse of the homogenous matrix (see this course, page 72, Ridig Body Motion – Homogeneous Transformations by Claudio Melchiorri).
I strongly recommend to read a course about homogeneous transformation (the one linked should be good).
I recall the equations in case the link is no more accessible.
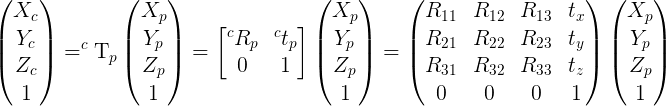
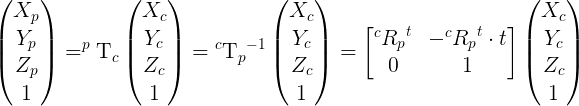
The superscript t in cRp^t simply means the transpose of matrix.
Note:
solvePnP() returning a rotation vector and a translation vector, you will have to use Rodrigues() to compute the rotation matrix from the rotation vector.