Revision history [back]

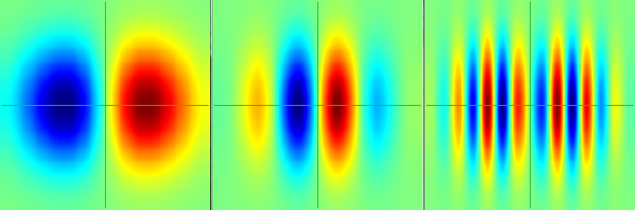
I was able to decode the strange behavior of the Gabor functions by keeping the other parameters constant in a more favorable position; This way, as seen from the graphic, the lambda parameter controls the frequency of the sinusoidal function that composes the kernel.

Conclusion: it controls the harmonic's frequency.

Bonus: The other parameters explained for non-math students:

psi - shift, in radians of the sinusoidal from center.

• 0 means that the max value in in center (symetrical, max positive)
• CV_PI/2 means that the max and min crescents are at the sides of the center (antisymetrical) - as in the above example
• CV_PI - min (negative value) in center (symetrical, max negative)

gamma - how elongated the filter is in the lateral direction. Seem to be the complement for the gaussian sigma, in the lateral direction. Note that low values mean elongated filters. 1 seem to a good default value.

sigma the good old sigma from the gaussian distribution. Controls the spread (radius)of the kernel

theta The rotation angle of the kernel. This way, you can select vertical stripes, horizontal stripes, or any other angle. It is the parameter of choice if you want to select, by example, edges at a given angle in an image. If you look for edges at 45 degrees, your gabor kernel will have to have a theta of pi/4

I was able to decode the strange behavior of the Gabor functions by keeping the other parameters constant in a more favorable position; This way, as seen from the graphic, the lambda parameter controls the frequency of the sinusoidal function that composes the kernel.

Conclusion: it controls the harmonic's frequency.

Edit This gorgeous answer from two math scholars shed some light on the strange pattern seen in the second graph. It's all about small details... here, numerical stability. Setting lambda to bigger values ( > 2) solves the issue. The comments are as useful as the post.

Bonus: The other parameters explained for non-math students:

psi - shift, in radians of the sinusoidal from center.

• 0 means that the max value in in center (symetrical, max positive)
• CV_PI/2 means that the max and min crescents are at the sides of the center (antisymetrical) - as in the above example
• CV_PI - min (negative value) in center (symetrical, max negative)

gamma - how elongated the filter is in the lateral direction. Seem to be the complement for the gaussian sigma, in the lateral direction. Note that low values mean elongated filters. 1 seem to a good default value.

sigma the good old sigma from the gaussian distribution. Controls the spread (radius)of the kernel

theta The rotation angle of the kernel. This way, you can select vertical stripes, horizontal stripes, or any other angle. It is the parameter of choice if you want to select, by example, edges at a given angle in an image. If you look for edges at 45 degrees, your gabor kernel will have to have a theta of pi/4

I was able to decode the strange behavior of the Gabor functions by keeping the other parameters constant in a more favorable position; This way, as seen from the graphic, the lambda parameter controls the frequency of the sinusoidal function that composes the kernel.

Conclusion: it controls the harmonic's frequency.

Edit

This gorgeous answer from two math scholars shed some light on the strange pattern seen in the second graph. It's all about small details... here, numerical stability. Setting lambda to bigger values ( > 2) solves the issue. The comments are as useful as the post.

Bonus: The other parameters explained for non-math students:

psi - shift, in radians of the sinusoidal from center.

• 0 means that the max value in in center (symetrical, max positive)
• CV_PI/2 means that the max and min crescents are at the sides of the center (antisymetrical) - as in the above example
• CV_PI - min (negative value) in center (symetrical, max negative)

gamma - how elongated the filter is in the lateral direction. Seem to be the complement for the gaussian sigma, in the lateral direction. Note that low values mean elongated filters. 1 seem to a good default value.

sigma the good old sigma from the gaussian distribution. Controls the spread (radius)of the kernel

theta The rotation angle of the kernel. This way, you can select vertical stripes, horizontal stripes, or any other angle. It is the parameter of choice if you want to select, by example, edges at a given angle in an image. If you look for edges at 45 degrees, your gabor kernel will have to have a theta of pi/4